Przejmowanie ciepła w szybach zespolonych

Wprowadzenie

Podstawowym parametrem do szacowania strat ciepła przez przegrody budowlane jest współczynnik przenikania ciepła U [W/m 2K]. Wielkość ta opisuje wymianę ciepła jednostki powierzchni przegrody przy jednostkowej różnicy temperatur powietrza po obu jej stronach.

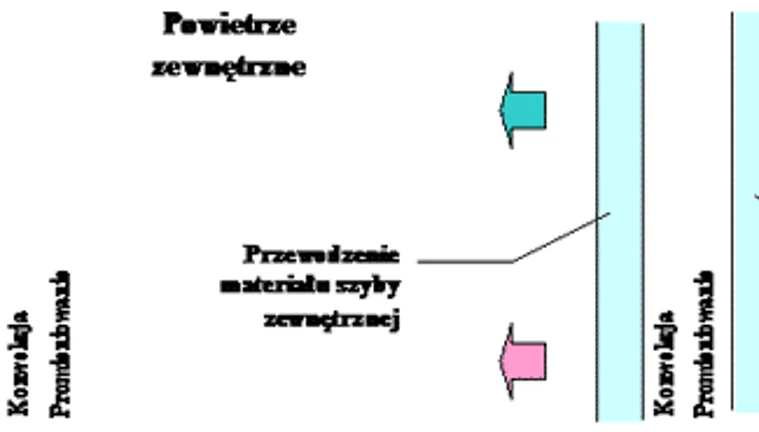
W przypadku szyby zespolonej (rys. 1) w obliczeniach U należy uwzględnić następujące czynniki:

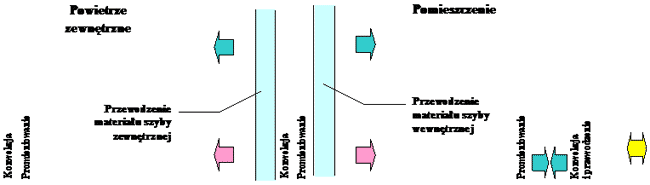Rys. 1. Schemat wymiany ciepła w szybie zespolonej

Według klasycznej teorii współczynnik U szyby zespolonej można wyznaczyć ze wzoru

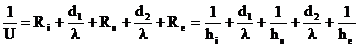gdzie: h i, h e - współczynnik przejmowania ciepła po wewnętrznej i zewnętrznej stronie szyby
zespolonej [W/(m 2K) ]; odwrotność tego współczynnika nazywamy oporem
przejmowania ciepła R i, R e [(m 2K) /W],

d 1, d 2 - grubość szyby wewnętrznej i zewnętrznej [m],

l - współczynnik przewodności cieplnej szkła, l = 1,0 W/mK,

h s - całkowita przewodność cieplna komory międzyszybowej [W/(m 2K)]; odwrotność
tej wielkości nazywamy oporem cieplnym komory R s [(m 2K) /W].

1. Przewodność cieplna komory międzyszybowej – uwarunkowania normowe

Wewnątrz zamkniętych szczelin powietrznych odbywa się złożony proces wymiany ciepła. Ciepło wymieniane jest przez przewodzenie i konwekcję gazu, oraz między powierzchniami szczeliny, przez promieniowanie.

W obliczeniach praktycznych najczęściej rozpatruje się przewodzenie i konwekcję łącznie a promieniowanie osobno. Całkowita przewodność cieplna komory h s wynosi więc

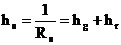gdzie: h g – przewodność cieplna warstwy gazu w komorze, z uwzględnieniem konwekcji
i przewodzenia, bez uwzględnienia promieniowania [W/(m 2K)],

h r – przewodność cieplna komory przez promieniowanie [W/(m 2K)].

Jeżeli mamy do czynienia ze szczeliną poziomą i przepływem ciepła z góry do dołu, gaz o mniejszej gęstości znajduje się w górnej części szczeliny i konwekcja w zasadzie nie występuje [1]. W przypadku szczeliny pionowej oraz poziomej, przy przepływie ciepła z dołu do góry, charakter wymiany ciepła zależy od szerokości szczeliny. Jeśli jest ona mała, gaz pozostaje w bezruchu lub przemieszcza się ruchem laminarnym (uporządkowanym). W tym przypadku przyjmuje się, że wymiana ciepła w gazie odbywa się tylko przez przewodzenie. W szerszej szczelinie nie można pomijać wpływu konwekcji na wymianę ciepła. Warunki graniczne określane są tzw. liczbą Nusselta Nu (patrz wzór 5).

Literatura [1, 2, 3] proponuje wprowadzenie równoważnego współczynnika przewodzenia ciepła gazu l r , zwiększającego współczynnik przewodzenia ciepła gazu l , bez uwzględnienia konwekcji. W takim przypadku przewodność cieplną warstwy gazu w komorze h g, z uwzględnieniem konwekcji, bez uwzględnienia promieniowania oblicza się ze wzoru

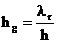gdzie: h – szerokość komory szyby zespolonej [m].

Wielkość l r/ l została wyznaczona eksperymentalnie. Niektóre zależności z literatury zebrano w tabeli 1.

Tabela 1. Wzory do wyznaczania równoważnego współczynnika przewodzenia ciepła gazu l r

Uwaga: b – wysokość komory (dla szyby ustawionej pionowo)

Gr, Pr ­ liczby kryterialne Grashofa i Prandtla (patrz wzór 6)

W aktualnie obowiązującej normie [4], dotyczącej obliczeń współczynnika przenikania ciepła U szyb zespolonych przyjęto, że jeśli obliczona dla danych warunków liczba Nusselta Nu jest mniejsza od 1, przepływ ciepła odbywa się tylko przez przewodzenie (w obliczeniach nie uwzględniamy Nu) – w przeciwnym wypadku w obliczeniach należy uwzględnić konwekcję. Wzór (28) przyjmuje postać

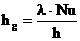gdzie: l – współczynnik przewodzenia ciepła gazu [W/(mK)].

Liczbę Nu określono wzorem

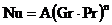gdzie: A,n – stałe przyjmowane dla przestrzeni pionowych A= 0,035; n= 0,38; pod kątem 45 0 A= 0,1; n= 0,31; poziomych przy przepływie ciepła do góry A= 0,16; n= 0,28;

Gr, Pr – liczby Grashofa i Prandtla

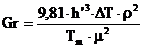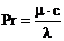gdzie: DT, T m – różnica temperatur między powierzchniami wewnątrzkomorowymi oraz średnia temperatura gazu w komorze [K],

r – gęstość gazu [kg/m 3],

m – lepkość dynamiczna gazu [kg/(m ×s)],

c – ciepło właściwe gazu [J/(kg ×K)].

Parametry gazów używanych do wypełniania przestrzeni gazowych w szybach zespolonych przedstawione są w normie [4].

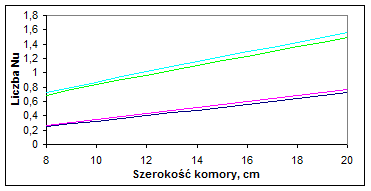
Na rys. 2 przedstawiono zależność Nu od szerokości przestrzeni gazowej w szybie, jej położenia oraz rodzaju gazu. Odnoszące obrazują graniczne szerokości komory, od których w obliczeniach należy uwzględniać konwekcję. Z przedstawionych wykresów wynika, że liczba Nu w niewielkim stopniu zależy od rodzaju gazu, natomiast silny jest wpływ położenia szyby.

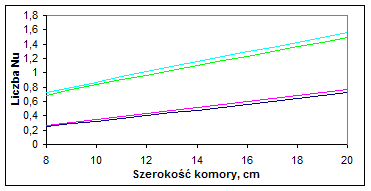Rys. 2. Zależność liczby Nusselta od charakterystyki przestrzeni gazowej

Jeśli chodzi o wpływ promieniowania na przewodność cieplną komory norma [4] zaleca posługiwanie się wzorem

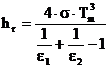gdzie: T m – średnia temperatura gazu w komorze [K],

s - stała Stefana-Bolzmanna 5,67 ´10 -6 W/m 2K 4,

e 1, e 2 – współczynniki emisyjności powierzchni wewnątrzkomorowych, dla szkła
bez napylenia można przyjmować 0,837.

Na rys. 3 i 4 przedstawiono obliczenia oporu cieplnego komory według założeń normy [4] przy założeniu zestawu szyb zwykłych i zestawu z jedną szybą niskoemisyjną o emisyjności e = 0,1. Można zauważyć, że wartości R ssą kilkakrotnie większe przy zastosowaniu szyb o niskiej emisji. Oznacza to znacznie większą izolacyjność cieplną tych szyb.

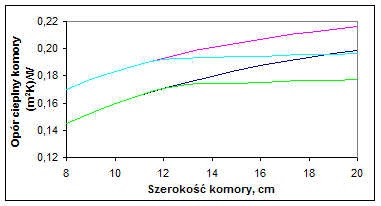Rys. 3. Zależność oporu cieplnego komory R s od charakterystyki przestrzeni gazowej

przy założeniu obydwu szyb ze szkła zwykłego, e 1= e 2 =0,837, oraz DT= 3K

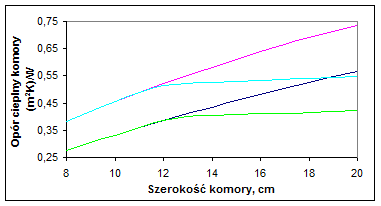Rys. 4. Zależność oporu cieplnego komory R sod charakterystyki przestrzeni gazowej

przy założeniu jednej z szyb niskoemisyjnej, e 1= 0,837; e 2 =0,1; oraz DT= 3K

2. Przejmowanie ciepła na zewnętrznych powierzchniach zestawu

Przejmowanie ciepła odbywa się również na zewnętrznych powierzchniach szyb zestawu. W tym przypadku mówimy o przejmowaniu ciepła przez konwekcję i promieniowanie:

h i(e) = h c + h r , (8)

gdzie: h e – współczynnik przejmowania ciepła po stronie powietrza zewnętrznego
zestawu [W/(m 2K)],

h i – współczynnik przejmowania ciepła od strony pomieszczenia [W/(m 2K)],

h c, h r – współczynnik przejmowania ciepła przez konwekcję oraz promieniowanie,
[W/(m 2K)].

Wielkość h c została wyznaczona eksperymentalnie. Niektóre zależności z literatury zebrano w tabeli 2. Przy przejmowaniu ciepła od strony pomieszczenia spotykamy się najczęściej z przypadkiem konwekcji swobodnej, od strony powietrza zewnętrznego mamy do czynienia z konwekcją wymuszoną spowodowaną wiatrem. Norma cieplna [5] zaleca, w obliczeniach przegród budowlanych, dla konwekcji swobodnej przyjmować wartości: 5,0; 2,5; 0,7 W/m 2K (odpowiednio dla ruchu ciepła w górę, poziomo i w dół) – dla konwekcji wymuszonej stosować zależność h c = 4 + 4 ×v.

Tabela 2. Wzory do wyznaczania współczynnika przejmowania ciepła przez konwekcję h c

Uwaga: D t – różnica między temperaturą powietrza a temperaturą powierzchni, 0 C,

t – temperatura powietrza, 0 C,

e p – współczynnik poprawkowy – dla -30 0 C ® e = 1,04; dla 30 0 C ® e = 0,96;

v – prędkość ruchu powietrza, m/s,

l – długość elementu w kierunku ruchu powietrza, m,

m – współczynnik poprawkowy – dla -30 0 C ® e = 1,06; dla 30 0 C ® e = 0,94;

Re = v × l / n – liczba kryterialna Reynolds’a,

n – lepkość kinematyczna powietrza – 13,28 × 10 -6 m 2/s.

Do wyznaczenia współczynnika przejmowania ciepła przez promieniowanie h rmożna używać wzoru ogólnego

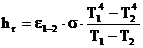gdzie: T 1 – temperatura powierzchni szyby [K],

T 2 – temperatura powierzchni przegród otaczających lub nieboskłonu, K,

s - stała Stefana-Bolzmanna 5,67 ´10 -6 W/m 2K 4,

e 1- 2 – emisyjność zastępcza wyznaczona na podstawie literatury przedmiotowej [3].

Norma [94] podaje wzór uproszczony

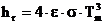gdzie: T m – średnia z temperatury powierzchni szyby i temperatury otoczenia [K],

e - emisyjność powierzchni.

Literatura